Ολα τα φαινομενα και ολο τον κοσμο γυρω μας προσπαθουμε να τον κατανοησουμε και να τον προβλεψουμε μεσω των μαθηματικων και της φυσικης.
Ενα απο τα γενικοτερα και ευρεως χρησιμοποιουμενα “εργαλεια” για αυτο, που μπορει να προβλεψει τις περισσοτερες κινησεις στον κοσμο μας, ειναι οι μερικες διαφορικες εξισωσεις. Απο το πως κινουνται οι πλανητες, το πως κινουνται τα μορια του αερα, την κινηση της ατμοσφαιρας που δημιουργει το κλιμα και τον καιρο, την ροη των θαλασσων, των ποταμων και γενικα του νερου, την ροη στον καπνο ενος τσιγαρου, το ποσο αεροδυναμικο ειναι ενα αυτοκινητο, την πτηση των αεροπλανων, την ακουστικη ολων των ειδων, την ροη θερμοτητας για οποιαδηποτε θερμαντικη συσκευη και γενικα αμετρητα άλλα φαινομενα οπου αλλαζουν μεσα στον χρονο και τον χωρο, η προβλεψη της εξελιξης τους βρισκεται με την επιλυση των καταλληλων μερικων διαφορικων εξισωσεων που τις διεπουν. Ετσι μπορουμε να ξερουμε με ακριβεια πότε δυει ο ηλιος, το πως θα κατασκευασουμε ενα πιο ασφαλες αεροπλανο ή αυτοκινητο, μπορουμε να κανουμε προβλεψη του καιρου πολλες μερες μετα, προβλεψη κλιματος πολλα χρονια μετα, να μελετησουμε την ατμοσφαιρικη ρυπανση, τα ρευματα του ωκεανου, να κατασκευασουμε ασφαλη πλοια, κλπ κλπ.
Το μεγαλο προβλημα ομως ειναι οτι συνηθως μια μερικη διαφορικη εξισωση ειναι απιστευτα δυσκολο να λυθει δινοντας μια αναλυτικη λυση. Ετσι, αναγκαζομαστε να εφευρισκουμε τροπους να βρεθουν προσεγγιστικα οι λυσεις με οσοδηποτε ακριβεια θελουμε. Η χρηση ομως αριθμητικων μεθοδων ειναι εξαιρετικα χρονοβορα τις περισσοτερες φορες και μερικες φορες μη πρακτικη(παρα πολυ μεγαλος χρονος επιλυσης).
Ενα συστημα τετοιων εξισωσεων ειναι οι λεγομενες Navier-Stokes εξισωσεις οι οποιες αποτελουν ενα εξαιρετικα σημαντικο εργαλειο σε παρα πολλους κλαδους(υδροδυναμικη, μετεωρολογια, κλιματολογια, αεροναυπηγικη, ναυπηγικη, αυτοκινητοβιομηχανιες και σε πολλους αλλους κλαδους) μιας και χρησιμοποιουνται για να περιγραψουν την κινηση των ρευστων. Αποτελουν ουσιαστικα εξειδικευση του 2ου νομου του Νευτωνα για την κινηση των ρευστων και ειναι απλως αναλυτικες εκφρασεις της αρχης διατηρησης της μαζας και της ορμης. Το προβλημα με αυτες τις εξισωσεις ειναι οπως και με ολες τις μερικες διαφορικες εξισωσεις οτι συνηθως ειναι παρα πολυ δυσκολο εως αδυνατο να βρουμε αναλυτικες λυσεις, οποτε αναγκαζομαστε να χρησιμοποιουμε αριθμητικες μεθοδους για την λυση τους.
Ειναι δε τοσο σημαντικο πεδιο ερευνας, λογω των απειρων εφαρμογων τους, οι εξισωσεις Navier-Stokes, που το ιδρυμα Clay Mathematics Institute προσφερει 1 εκατομμυριο δολαρια σε οποιον καταφερει να απαντησει στο ερωτημα εαν υπαρχει για καθε συστημα εξισωσεων Navier-Stokes μια ομαλη λυση στον τριδιαστατο χωρο ή εαν γινει αποδειχτει οτι υπαρχουν συστηματα που δεν εχουν ομαλες λυσεις.
Μιας και λοιπον δεν εχουμε αναλυτικο τροπο λυσεως τους, αναλωνομαστε σε αριθμητικες λυσεις που ομως απατουν τεραστια υπολογιστικη ισχυ ακομα και για απλα προβληματα. Ετσι ειναι απαραιτητη η χρηση των λεγομενων supercomputers, που κοστιζουν δισεκατομμυρια δολαρια, για να επιτυχουμε λυσεις σε πρακτικο χρονο.
Τα τελευταια 3.5 χρονια ομως επηλθε μια αλματωδη αναπτυξη καποιων νεων μεθοδων τεχνητης νοημοσυνης, βασει “βαθιας μαθησης”(deep learning) εκπαιδευοντας τεχνητα νευρωνικα δικτυα(artificial neural networks ή ΑΝΝ), οπου εφερε πραγματικη κοσμογονια και τεραστια αλματα μπροστα σε παρα πολλους τομεις, οπου αναμεναμε να τα δουμε 10 και 20 χρονια στο μελλον και τα βλεπουμε τωρα.
Ετσι στο Caltech, το Ινστιτουτο Τεχνολογιας της Καλιφορνιας, αναπτυχθηκε προσφατα μια πρωτοπορα μεθοδος deep learning για την επιλυση μερικων διαφορικων εξισωσεων με 3 τεραστια πλεονεκτηματα οπως αναφερουν στα αποτελεσματα τους στο paper της δημοσιευσης τους που δωθηκε στην δημοσιοτητα πριν μερικες ημερες. Με την νεα αυτη λοιπον deep learning μεθοδο εχουμε την δυνατοτητα τα εκπαιδευμενα ΑΝΝ να δινουν πολυ πιο ακριβεις λυσεις στις εξισωσεις μας, ενω και η δυνατοτητα γενικευσης ειναι μεγαλυτερη χωρις μαλιστα να ειναι αναγκαια η επανεκπαιδευση για την επιλυση συστηματων εξισωσεων που ανηκουν στην ιδια οικογενεια. Και επιπροσθετως και πιο σημαντικο, εχουν και το εκπληκτικο πλεονεκτημα του οτι ειναι 3 ταξεις μεγεθους ταχυτερα απο τις εως τωρα πιο γρηγορες μεθοδους επιλυσης! 3 ταξεις μεγεθους πιο γρηγορα σημαινει περιπου 1000 φορες ταχυτερα!
Τα πλεονεκτηματα ειναι σαφες τι σημαινουν. Οτι καταρχην η αναγκη για χρηση πανακριβων supercomputer για την επιλυση προβληματων που λυνονται με μερικες διαφορικες εξισωσεις δεν ειναι τοσο μεγαλη, ενω και υποχιλιαπλασιαζοντας τον χρονο επιλυσης θα μπορουμε πλεον να λυσουμε πολυ περισσοτερες εξισωσεις(1000 φορες περισσοτερες για την ακριβεια) στον ιδιο χρονο! Επισης λογω του οτι κερδιζουμε 1000 φορες σε ταχυτητα θα μπορουμε να αυξησουμε την αναλυση(την κλιμακα, δηλαδη το πόσες λεπτομερειες θα βλεπει η μοντελοποιηση μας) πολλες φορες και να εχουμε καλυτερη προσεγγιση στο προβλημα. Και ετσι και αλλιως η ακριβεια αυτης της νεας μεθοδου ειναι καλυτερη.
Οποτε πχ στον καιρο, θα μπορουμε να εχουμε πολυ καλυτερη μοντελοποιηση των προβληματων ανωμεταφορας(convection), των καταιγιδων πχ που εως τωρα μόνο με εξαιρετικα προσεγγιστικες μεθοδους τις αντιμετωπιζαμε. Για αυτο και οι αστοχιες στην προβλεψη καταιγιδων και των παραμετρων τους παραμενουν ακομα μεγαλο προβλημα. Οπως βεβαια και να εισαγουμε πολυ καλυτερη αναλυση στα καιρικα και κλιματολογικα μοντελα μιας και η ταχυτητα που η μεθοδος αυτη μας επιτρεπει να κερδιζουμε θα μας το επιτρεπει ωστε να επιλυουμε τις εξισωσεις στον ιδιο χρονο ή και συντομοτερα με πολυ μεγαλυτερη ακριβεια στην προσομοιωση μας της ατμοσφαιρας.
Ετσι, εαν αποδειχτει και απο αλλους ερευνητες η τεραστια αποτελεσματικοτητα της μεθοδου που αναφερεται στο paper, η βελτιωση στα καιρικα μοντελα και στα κλιματικα μοντελα θα ειναι πολυ μεγαλη! Ετσι πχ τα κλιματολογικα μοντελα θα μπορουν να τρεχουν με πολυ καλυτερες χωρικες αναλυσεις αφου ο χρονος που θα χρειαζεται να τρεξουν δεν θα ειναι απαγορευτικος.
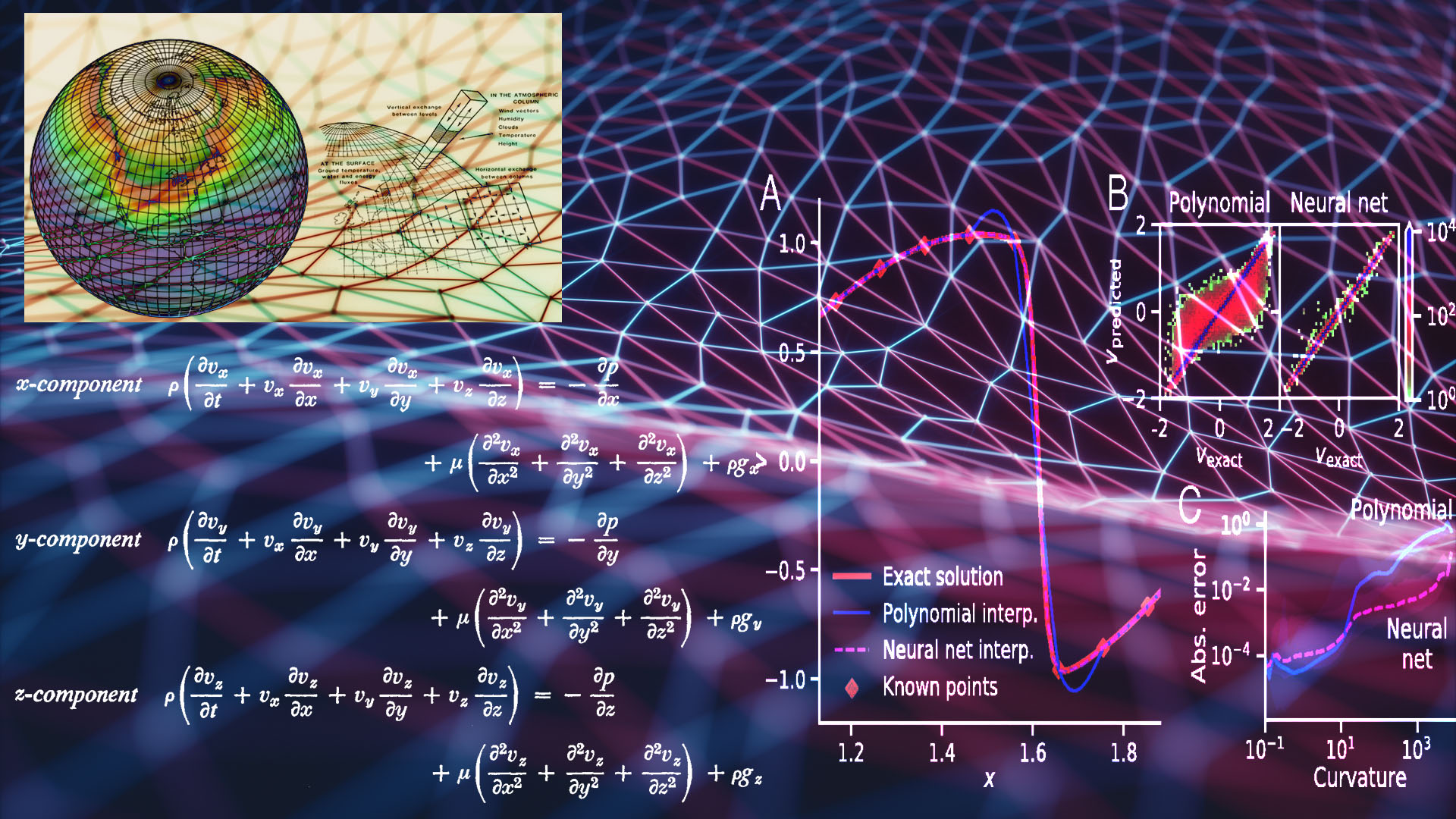
Παρακατω φαινονται 2 διαφορετικες καταστασεις ενος ρευστου στην 1η στηλη. Στην 2η στηλη η πραγματικη πορεια που ακολουθησε το ρεσυτο και στην 3η στηλη η προβλεψη του ΑΝΝ με την μεθοδο αυτη για το πως θα κινηθει το ρευστο. Οπως φαινεται η προβλεψη απεχει πολυ λιγο απο την πραγματικοτητα.
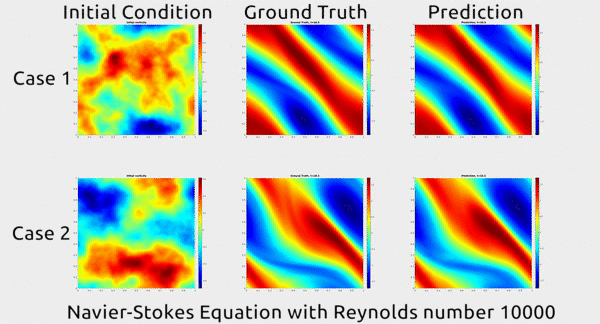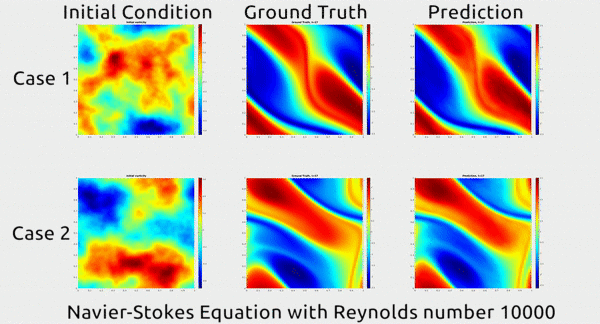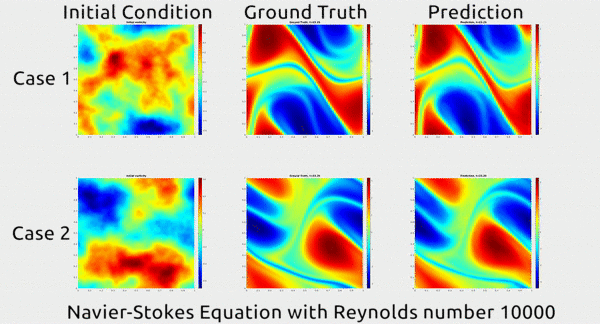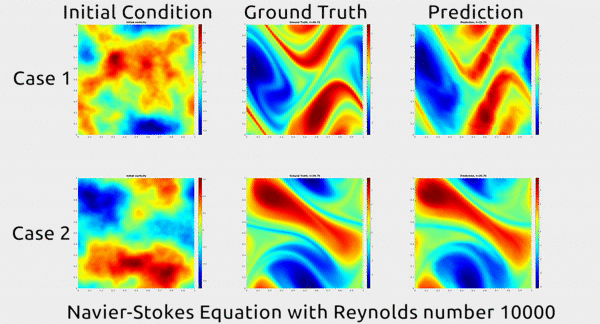
Η τεχνικη για να το πετυχουν αυτο ηταν πολυ εξυπνη. Στις συνηθεις μεθοδους με ΑΝΝ για επιλυση εξισωσεων, τα ΑΝΝ εκπαιδευονται να προσεγγιζουν συναρτησης στον Ευκλειδιο χωρο και η απεικονιση μεταξυ εισοδου και εξοδου γινεται σε αυτον τον χωρο. Στην νεα αυτη τεχνικη ομως χρησιμοποιησαν τον χωρο Φουριέ για την απεικονιση, οριζοντας τις συναρτησεις σε αυτον τον χωρο θεωρωντας οτι ο αερας και η κινηση του μπορει να περιγραφει ως αθροισμα πολλαπλων συχνοτητων κυματων που αναπαριστουν την κινηση του αερα. Αυτη η θεωρηση αποδεικνυεται οτι ειναι πολυ πιο αποτελεσματικη στο να εκπαιδευτει ενα ΑΝΝ.
Μια απο τους ερευνητες του paper, η Anima Anandkumar λεει οτι ειναι πολυ ενθουσιασμενη να δει την εφαρμογη της μεθοδου τους στο τομεα της κλιματικης αλλαγης και του καιρου. Καθως οι εξισωσεις Navier-Stokes δεν ειναι καλες μόνο στο να προβλεπουν την κινηση των αεριων μαζων αλλά και στην προβλεψη των διαφόρων πατερν κυκλοφοριας.
Μπορει ολα αυτα να ακουγονται υπερβολικα ωραια και ενθαρρυντικα, αλλά απομενει να αποδειχτει οτι δουλευουν και στην πραξη, με την εφαρμογη τους σε διάφορους τομεις. Το κοντινο μελλον θα δειξει….
Οι ελπιδες παντως ειναι μεγαλες, μιας και τα ΑΝΝ με τις νεες μεθοδους deep learning εχουν φερουν πραγματικη κοσμογονια σε πολλους τομεις της επιστημης την τελευταια 3ετια.
Η ερευνα:
Fourier Neural Operator for Parametric Partial Differential Equations
Zongyi Li, Nikola Kovachki, Kamyar Azizzadenesheli, Burigede Liu, Kaushik Bhattacharya, Andrew Stuart, Anima Anandkumar
https://arxiv.org/abs/2010.08895